Я всегда говорил своему другу, что математика со своими изящными абстракциями обладает той магической силой, потенциал которой до сих пор полностью не раскрыт. Сегодня я хочу поговорить о том, как можно приблизить число Пи с помощью множества Мандельброта.
Пару слов о множестве
На самом деле на Хабре куча статей, описывающие множество Мандельброта (далее, множество М), рассматривающие его свойства, историю и удивительную красоту, подкрепляя всё это красочными картинками. Мне бы не хотелось останавливаться на его определении и прочих деталях, а сразу перейти к делу. Однако в силу того, что оно является центральным субъектом данной статьи, я все же освежу вашу память.
Множество М — это множество всех комплексных чисел с, для которых функция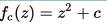 
при ее итерации с 
ограничена. Настолько просто.
На практике мы применяем следующую теорему: если функция (вышеприведенная) в ходе итерации превосходит значение 2, то она 100% не ограничена. Поэтому, определить множество можно так:
Главная 
